Construction calculators » Diagrams of normal and shear stresses online

Build diagrams of normal and longitudinal stresses

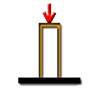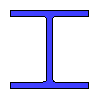
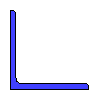
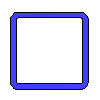
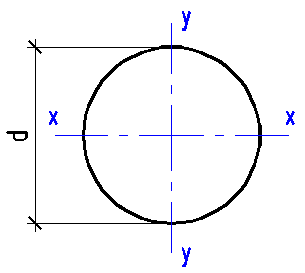
Data input:

Diameter d mm

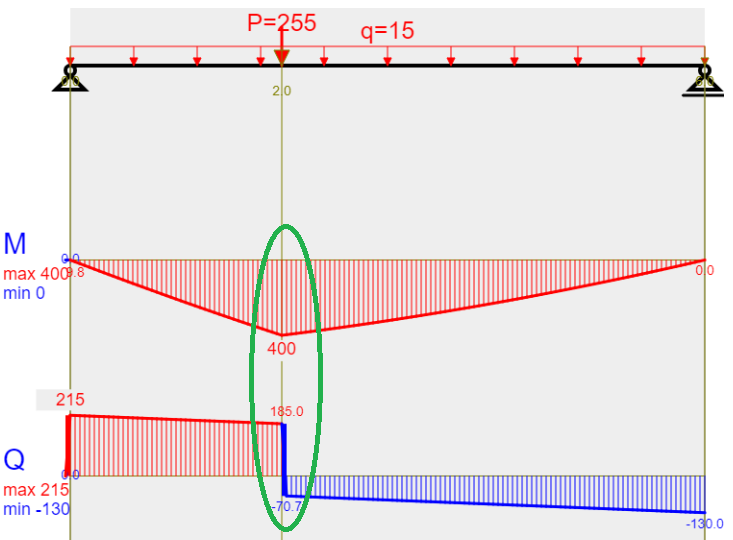
Moment M

Shear force Q

Name	Value, MPa
Maximum normal stresses	{{max_sigma}}
Maximum shear stresses	{{max_j}}

find out stresses along the height of the section

Distance from center mm

Name	Value, MPa
Normal stresses	{{sigma}}
Shear stresses	{{j}}
Total stresses	{{napr_all}}

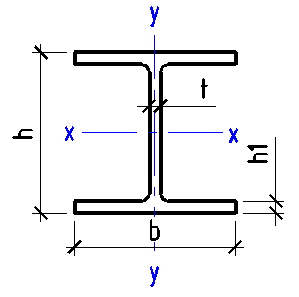
Data input:

Height h mm

Width b mm

Wall thickness t mm

Flange height h1 mm

Moment M

Shear force Q

Name	Value, MPa
Maximum normal stresses	{{max_sigma}}
Maximum shear stresses	{{max_j}}

find out stresses along the height of the section

Distance from center mm

Name	Value, MPa
Normal stresses	{{sigma3}}
Shear stresses	{{j3}}
Total stresses	{{napr_all3}}

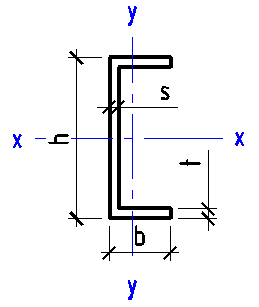
Data input:

Height h mm

Width b mm

Wall thickness s mm

Flange thickness t mm

Moment M

Shear force Q

Name	Value, MPa
Maximum normal stresses	{{max_sigma}}
Maximum shear stresses	{{max_j}}

find out stresses along the height of the section

Distance from center mm

Name	Value, MPa
Normal stresses	{{sigma4}}
Shear stresses	{{j4}}
Total stresses	{{napr_all4}}

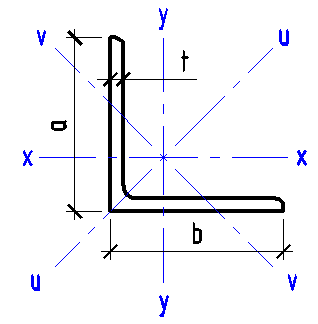
Data input:

Length a mm

Length b mm

Thickness t mm

Moment M

Shear force Q

Name	Value, MPa
Maximum normal stresses	{{max_sigma}}
Maximum shear stresses	{{max_j}}

find out stresses along the height of the section

Distance from center mm

Name	Value, MPa
Normal stresses	{{sigma5}}
Shear stresses	{{j5}}
Total stresses	{{napr_all5}}

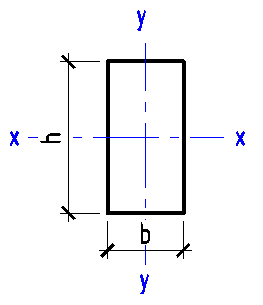
Data input:

Width b mm

Height h mm

Moment M

Shear force Q

Name	Value, MPa
Maximum normal stresses	{{max_sigma}}
Maximum shear stresses	{{max_j}}

find out stresses along the height of the section

Distance from center mm

Name	Value, MPa
Normal stresses	{{sigma6}}
Shear stresses	{{j6}}
Total stresses	{{napr_all6}}

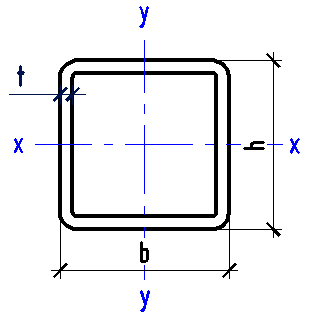
Data input:

Height h mm

Width b mm

Thickness t mm

Moment M

Shear force Q

Name	Value, MPa
Maximum normal stresses	{{max_sigma}}
Maximum shear stresses	{{max_j}}

find out stresses along the height of the section

Distance from center mm

Name	Value, MPa
Normal stresses	{{sigma7}}
Shear stresses	{{j7}}
Total stresses	{{napr_all7}}

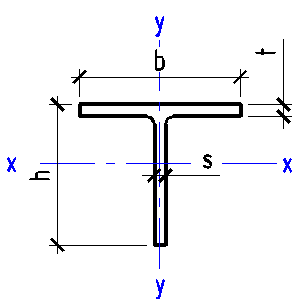
Data input:

Height h mm

Width b mm

Thickness t mm

Thickness s mm

Moment M

Shear force Q

Name	Value, MPa
Maximum normal stresses	{{max_sigma}}
Maximum shear stresses	{{max_j}}

find out stresses along the height of the section

Distance from center mm

Name	Value, MPa
Normal stresses	{{sigma8}}
Shear stresses	{{j8}}
Total stresses	{{napr_all8}}

This calculator is designed for calculating normal and shear stresses of various cross-sections, such as circular, I-beam, channel, angle, rectangular, hollow section, and T-beam.

Based on the constructed stress diagrams, you can determine the weakest points of the cross-section along its height by inputting the bending moment and shear force and comparing them with the calculated resistance of the beam material.

The bending moment (M) and shear force (Q) are determined as follows:

The most critical cross-section of the beam is highlighted in green. In this section, the maximum bending moment is M = 400 and the shear force is Q = 185 + 70.7 = 255.7.

Instructions:

Select the type of cross-section (circular, I-beam, channel, angle, rectangular, hollow section, or T-beam).
Enter the geometric characteristics of the cross-section.
Specify the bending moment (M) in the chosen units of measurement.
Enter the shear force (Q) in the chosen units of measurement.
Click the "Calculate" button.

The result will include the constructed diagrams of normal and shear stresses, as well as an image of the cross-section.

For convenience, the maximum stress values (in MPa) will be displayed in the table below.

If needed, you can determine the stress at any point along the height of the cross-section. To do this, check the "Determine stress by height" box and specify the distance from the centroid (marked by the red dashed line) to the desired point.

Additional information:
- Overall stresses are calculated using the third strength theory.
- To determine the bending moment M and shear force Q, use this calculator.